슐레플리 부호
덤프버전 :
분류
1. 개요[편집]
Schläfli 符號, Schläfli symbol
정다면체나 테셀레이션(또는 타일링)을 쉽게 표기하기 위해 개발된 부호 체계로, 19세기 기하학에 공헌한 수학자 루드비히 슐레플리(Ludwig Schläfli, 1814 ~ 1895)의 이름을 땄다.
2. 정다각형[편집]
2.1. 볼록 정다각형[편집]
정다각형들 중에서도 볼록 정다각형의 경우, 중괄호 안에 숫자 하나만 써 놓으면 슐레플리 부호로 괄호 속의 숫자만큼의 변이 있는 다각형을 의미한다. 따라서 평면 도형들 중 정다각형, 특히 볼록 정다각형을 표기하는 것은 매우 쉽다.
2.2. 오목 정다각형(별 정다각형)[편집]
오목 정다각형은 {n/m} 꼴로 표현하는데, 여기서 m은 이 다각형에서 꼭지점을 이을 때 m-1개의 꼭지점을 건너뛰어 연결한다는 뜻이다.
이렇게 표기하면 정다각형의 한 내각의 크기를 구하는 공식 [math(\displaystyle180\degree\times\frac{n-2}{n})]를 유리수로 확장하여 적용할 수 있어 매우 편리하다.
2.3. 음의 정다각형[편집]
다소 어렵다고 느낄 수도 있으니, 이해가 되지 않는다면 우선 아래의 3번 문단 "정다면체 및 테셀레이션"부터 읽고 오자.
정다각형을 이어 붙여 다면체를 만들 때, 일부 정다각형을 뒤로 꺾어 접어 만들 수도 있다. 이 때 음의 정다각형을 도입하면 꼭지점 형태를 매우 간단하게 표현할 수 있다.
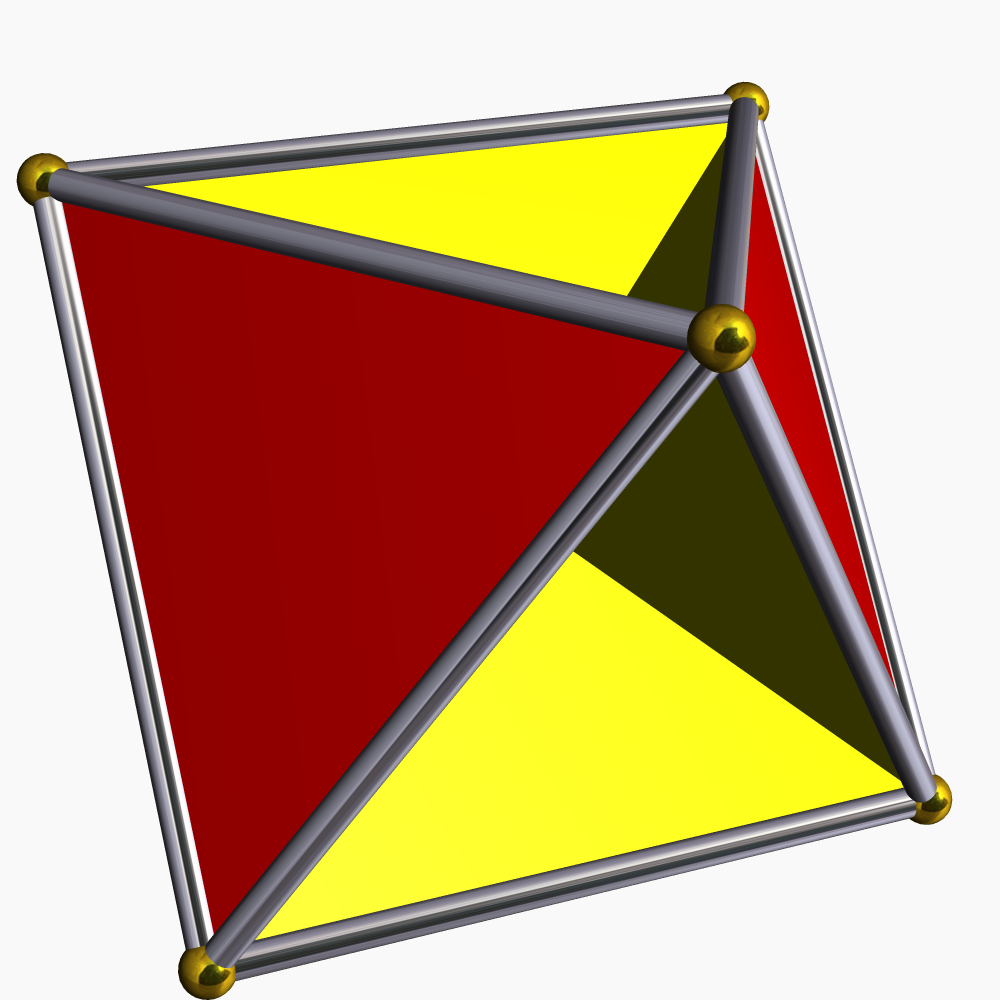
예를 들어 위와 같은 도형(사면반육면체)에서 한 꼭지점에 정삼각형-정사각형-음의 정삼각형-정사각형 순서로 배열되어 있다고 표현하면 자연스럽게 설명이 된다.
한 각이 [math(-\theta)]인 음의 [math(n)]각형을 {k}로 표현해보자. (단, [math(n, k)]는 양의 유리수)
[math(\theta=\displaystyle180\degree\times\frac{n-2}{n},\quad\displaystyle180\degree\times\frac{k-2}{k}=-\theta)]
이므로,
[math(\displaystyle180\degree\times\frac{k-2}{k}=-180\degree\times\frac{n-2}{n})]
에서
[math(\displaystyle k=\frac{n}{n-1})]가 된다. (n이 정수가 아닌 유리수여도 성립한다.)
따라서 음의 정n각형은 {n/(n-1)}각형으로 표현할 수 있으며, 한 각이 -60º인 음의 정삼각형의 경우 {3/2}가 되고, 위의 사면반육면체의 꼭지점 형태는 3.4.3/2.4로 표현할 수 있다.
슐레플리 부호가 {5/2}인 정오각별과 같이 n이 정수가 아닌 유리수일 경우, [math(\displaystyle n=\frac{p}{q})]라고 하면
[math(\displaystyle k=\frac{p/q}{p/q-1}=\frac{p}{p-q})]가 되어
음의 정오각별은 {5/3}으로 표현된다. 즉, (분모)를 (분자-분모)로 바꿔주기만 하면 된다.
2.4. 그 이외의 정다각형[편집]
{4/5}, {2/3}, {-1/2}같은 것들이 있다. 이들은 볼록 정다각형, 오목 정다각형, 음의 정다각형 중 어디에도 속하지 않는다.
3. 정다면체 및 테셀레이션[편집]
정다면체나 정규 테셀레이션을 {p,q}와 같이 쓰는데, 이는 "정p각형이 한 꼭지점에서 q개 모여 만들어지는 도형"이라는 의미이다.
유클리드 공간 도형의 경우, 한 꼭지점에 모이는 다각형들의 내각의 합이 360º 미만이면 접혀져 3차원 부피 공간을 차지하는 정다면체가 되며, 정확히 360°면 평면으로 축퇴되어 하나의 정다각형으로 평면을 채우는 "정규 테셀레이션"을 만들 수 있다. 360°를 초과할 경우 유클리드 공간에 나타낼 수 없다.
따라서 유클리드 공간에서 나타낼 수 있는 것은 볼록 5종, 오목 4종, 정규 테셀레이션 3종이며, 다음과 같이 쓸 수 있다.
유클리드 공간에 한정하면 위와 같이 12종에 불과하나, 구면 또는 구면 공간으로 확장하면 이각형을 사용해 무수히 많은 호조헤드론과 이면체를 만들 수 있으며, 쌍곡면, 또는 쌍곡 공간으로 개념을 확장하면 정p각형의 한 각의 크기가 [math(\frac{p-2}{p}\times 180\degree)]보다 작아지므로 {6,4}와 같이 유클리드 평면/공간에서 불가능한 정규 테셀레이션의 개념도 만들 수 있다.
이를 표로 만들면 아래와 같다.
* {p,1}, {1,q}은 p=2, q=2를 제외하면 존재하지 않음.
* ||<bgcolor=#acf,#228> {p,q} ||구면 테셀레이션만 존재||
||<-2>p=2 일 때: 호조헤드론
||
q=2 일 때 : 이면체
[3]* ||<bgcolor=#afa,#282> {p,q} ||정다면체 (또는 구면 테셀레이션)||
* ||<bgcolor=#fea,#ca0> {p,q} ||평면 테셀레이션||
||<-2>(p,q ≠ ∞) : 컴팩트 평면 테셀레이션
{2,∞} 또는 {∞,2} : 논컴팩트 평면 테셀레이션||* ||<bgcolor=#faa,#822> {p,q} ||쌍곡 테셀레이션||
||<-2>(p,q ≠ ∞) : 컴팩트 쌍곡 테셀레이션
{p,∞} 또는 {∞,q} : 파라컴팩트 쌍곡 테셀레이션||
3.1. 추상적 오목 테셀레이션[편집]
m이 3 이상의 자연수일 때, {n/m,n}, {n,n/m}, {n/m,3}, {3,n/m}이나 p가 4 이상의 자연수일 때, {n/2,p}, {p,n/2}, {n/m,p}, {p,n/m} 계열은 쌍곡의 각도가 나오더라도 추상적인지라, 선을 그을 때 무한히 겹치지 않고 만들 수 없다. 그래서 {10/3,10}, {9/2,4}, {11/2,4}, {11/3,11}, {11/4,11}, {13/3,13}, {19/3,3}, {20/3,3}, {25/4,3} 등등이나 이들의 쌍대들도 역시 만들어질 수 없다. 심지어 {5/2,11}, {7/2,5}, {7/3,15}, {8/3,9}, {9/2,4}, {9/4,19}, {10/3,6} 등등과 같은 계열이나 이들의 쌍대에 해당하는 도형 처럼 한 꼭짓점에서의 이포각의 합이 360°를 초과하더라도 만들 수 없어 추상적인 쌍곡이 무수히 많이 존재한다. 물론 {5/2,5/2}, {5/2,4}, {5/2,6}, {5/2,7}, {7/2,3}, {7/2,5/2}, {7/2,7/2}, {7/2,4}, {7/3,7/3}, {7/3,7/2} {7/3,3}, {7/3,4}, {7/3,5}, {8/3,5/2}, {8/3,7/2}, {8/3,7/3}, {8/3,8/3}, {8/3,4}, {8/3,5}, {9/2,5/2}, {9/2,7/2}, {9/2,7/3}, {9/2,8/3} {9/2,3}, {9/4,5/2}, {9/4,7/2}, {9/4,7/3}, {9/4,8/3}, {9/4,9/2}, {9/4,9/4}, {9/4,4}, {9/4,5}, {9/4,6}, {10/3,5/2}, {10/3,7/2}, {10/3,7/3}, {10/3,8/3}, {10/3,9/2}, {10/3,9/4}, {10/3,3}, {10/3,4} 등등과 같은 계열이나 이들의 쌍대들 같은 경우는 모든 내각의 합이 360°보다 작아서 쌍곡 벌집을 만들 수는 없다. 그리고 {5/2,10}, {7/2,14/3}, {7/3,14}, {8/3,8}, {9/2,18/5}, {9/4,18}, {10/3,5}, {11/2,22/7}, {11/3,22/5}, {11/4,22/3}, {11/5,22}, {12/5,12} 등등의 계열 및 이들의 쌍대들과 같이 {m/n,p/q}에서 (m/n-2)ㆍ(p/q-2)=4가 되는 계열들은 오목 유클리드 벌집이 되지만, 이들은 전부 만들 수 없게 된다. 따라서 실제로 가능한 유클리드 벌집 및 파라콤팩트는 볼록한 형태만 존재한다.
4. 4차원 정다포체 및 3차원 벌집[6][편집]
{p,q,r}과 같이 나타내며, {p,q}는 해당 도형을 이루고 있는 정다면체를 의미하며, r은 한 모서리에 정다면체가 몇 개 모였는지를 의미한다. 동시에 {q,r}은 이 정다포체/벌집 꼭지점의 단면 형태를 나타낸다.
4차원 공간에서는 단 하나의 정규 벌집{4,3,4}만 존재하며 3차원 공간을 꽉 채운다.
6개의 볼록 정다포체와 10개의 오목 정다포체가 존재한다.
- 4차원 볼록 정다포체
- 4차원 오목 정다포체
- {5/2,3,3} (큰 거대 별모양 백이십포체, Great Grand Stellated 120-cell)
- {5/2,3,5} (큰 별모양 백이십포체, Great Stellated 120-cell)
- {5/2,5,5/2} (거대 별모양 백이십포체, Grand Stellated 120-cell)
- {5/2,5,3} (작은 별모양 백이십포체, Small Stellated 120-cell)
- {3,5/2,5} (큰 이십면체 백이십포체, Great Icosahedral 600-cell)
- {3,3,5/2} (거대 육백포체, Grand 600-cell)
- {3,5,5/2} (정이십면체 백이십포체, Icosahedral 120-cell)
- {5,5/2,3} (큰 거대 백이십포체, Great Grand 120-cell)
- {5,5/2,5} (큰 백이십포체, Great 120-cell)
- {5,3,5/2} (거대 백이십포체, Grand 120-cell)
- 4차원 정규 벌집
- {4,3,4} 정육면체 벌집
테셀레이션과 마찬가지로, 비유클리드 초공간으로 개념을 확장하면 {5,3,4}, {3,5,3}와 같이 유클리드 초공간에서 불가능한 정다포체/정규 벌집도 가능하다. 다만 {6,3,3}, {3,6,3}, {4,4,3}, {4,4,4} 등과 그것들의 쌍대인 파라콤팩트나 {5,4,3}, {4,5,3}, {3,4,5}, {3,5,4} 등과 그것들의 쌍대인 논콤팩트는 n-1차원의 도형이나 꼭짓점을 끝까지 그릴 수가 없기에 푸앵카레 원반에서도 제대로 나타낼 수 없어진다. 특히 n-1차원 도형 혹은 꼭짓점도 파라콤팩트이거나 논콤팩트인 경우 유클리드 공간에서는 아예 만들 수가 없다.
5. 5차원 정다포체 및 4차원 벌집[편집]
{p,q,r,s}과 같이 나타낸다.
- 5차원 공간에서는 3개의 정규 벌집{4,3,3,4}, {3,4,3,3}, {3,3,4,3}이 존재하며 4차원 공간을 꽉 채운다.[7]
- 5차원 이상에서는 오직 3가지의 정다포체만이 존재한다.
- 5차원 볼록 정다포체
- 5차원 정규 벌집
- {4,3,3,4} 정팔포체 벌집
- {3,4,3,3} 정이십사포체 벌집
- {3,3,4,3} 정십육포체 벌집
- 5차원 오목 쌍곡 벌집
- {5/2,5,3,3}
- {3,3,5,5/2}
- {5,5/2,5,3}
- {3,5,5/2,5}
6. 6차원 이상의 정다포체 및 하위 차원 벌집[편집]
{p,q,r,s,t,...}과 같이 나타낸다.
- n (n ≥ 6)차원 볼록 정다포체
- {3,3,...,3,3} (n-단체)[8]
- {4,3,...,3,3} (n-초입방체)
- {3,3,...,3,4} (n-정축체)
- n - 1차원 정규 벌집
- {4,3,...,3,4} n - 1 입방체 벌집
7. 관련 문서[편집]
 이 문서의 내용 중 전체 또는 일부는 2023-12-04 15:35:23에 나무위키 슐레플리 부호 문서에서 가져왔습니다.
이 문서의 내용 중 전체 또는 일부는 2023-12-04 15:35:23에 나무위키 슐레플리 부호 문서에서 가져왔습니다.[1] 벌집(honeycomb) : 공간, 또는 초공간을 다포체를 사용하여 빈틈 없이 채운 것. 말 그대로 벌집이라는 뜻이다.[2] 3차원이라고 적지 않는 이유는, 테셀레이션들은 평면 또는 구면, 쌍곡면으로 축퇴되어 2차원으로 구현할 수 있기 때문이다.[3] {2,2}는 이각이면체이자 이각호조헤드론인 자기쌍대 도형으로, 유일하게 이면체이면서 호조헤드론인 도형이다.[4] n=5일 경우 접혀져 큰 십이면체가 된다.[5] n=5일 경우 접혀져 작은 별모양 십이면체가 된다.[6] 벌집(honeycomb) : 공간, 또는 초공간을 다포체를 사용하여 빈틈 없이 채운 것. 말 그대로 벌집이라는 뜻이다.[7] 6차원 이상은 무조건 1개의 벌집만이 존재하며 n-1차원을 덮는다.[8] ... 부분에는 차원에 맞는 개수의 3이 들어간다. 예시: 6-초입방체 = {4,3,3,3,3}, 7-정축체 = {3,3,3,3,3,4}[9] 깎기, 절반깎기, 부풀리기, 부풀려 깎기, 다듬기가 있으며, 절반깍기를 이용해서 만든 정다면체는 서로 쌍대 관계인 두 다면체의 면을 한 쌍 합쳐놓은 꼴이며, 이를 또 절반깍기할 경우에는 부풀리기가 되는 것이다. 뿐만 아니라 이는 쌍곡 벌집이나 4차원 이상의 정다포체, 유클리드 벌집, 쌍곡 벌집, 심지어는 오목 다포체나 벌집(가능한 것, 불가능 한 것 모두 해당)에도 그대로 적용할 수 있다.