브링 근호

덤프버전 :

분류

특수함수
Special Functions

[ 펼치기 · 접기 ]
적분
오차함수(error function) · 베타 함수(불완전 베타 함수) · 감마 함수(불완전 감마 함수 · 로그 감마 함수) · 타원 적분 · 야코비 타원 함수 · 지수 적분 함수 · 로그 적분 함수 · 삼각 적분 함수 · 쌍곡선 적분 함수 · 프레넬 적분 함수 · 구데르만 함수
미분방정식
르장드르 함수* · 구면 조화 함수 · 베셀 함수 · 에르미트 함수 · 라게르 함수 · 에어리 함수
역함수
브링 근호 · 람베르트 [math(W)] 함수 · 역삼각함수
급수
제타 함수 · 세타 함수 · 초기하함수 · 폴리로그함수 · 바이어슈트라스 타원 함수
정수론
소수 계량 함수 · 소인수 계량 함수 · 뫼비우스 함수 · 최대공약수 · 최소공배수 · 약수 함수 · 오일러 파이 함수 · 폰 망골트 함수 · 체비쇼프 함수 · 바쁜 비버 함수
기타
헤비사이드 계단 함수 · 부호 함수 · 테트레이션(무한 지수 탑 함수) · 집합 판별 함수 · 바닥함수 / 천장함수 · 허수지수함수 · 혹 함수
* 특수함수가 아니라 특정 조건을 만족시키는 다항함수이지만, 편의상 이곳에 기술했다.




브링 근호(Bring radical) 또는 초근호(ultraradical)[1]는 특수함수의 일종으로, [math(\mathrm{BR}(x))]로 표기한다. 오차 방정식(quintic equation)

[math(x^5+x+a=0 )]
[1] 공식 역어는 아니다. 이렇게 표현한 이유는 이미 초제곱근이라고 불리는 함수([math(\sqrt{x}_s = e^{(W \circ\,\ln)(x)})],테트레이션의 역함수)가 따로 있기 때문이다. 여기서 [math(W)]는 람베르트 [math(W)] 함수이다.

의 실근을 [math(\mathrm{BR}(a))]로 표기한다. [math(\mathrm{BR}(x))]의 정의는 다음과 같다.

[math(\mathrm{BR}(x) = -x \cdot {}_4{F}_3 \!\left(\dfrac{1}{5},\,\dfrac{2}{5},\,\dfrac{3}{5},\,\dfrac{4}{5};\,\dfrac{1}{2},\,\dfrac{3}{4},\,\dfrac{5}{4};\,-5\left(\dfrac{5x}{4}\right)^4\right))]

여기서 [math({}_4{F}_3)]은 초기하함수이다. 해당 함수의 그래프는 아래와 같다.

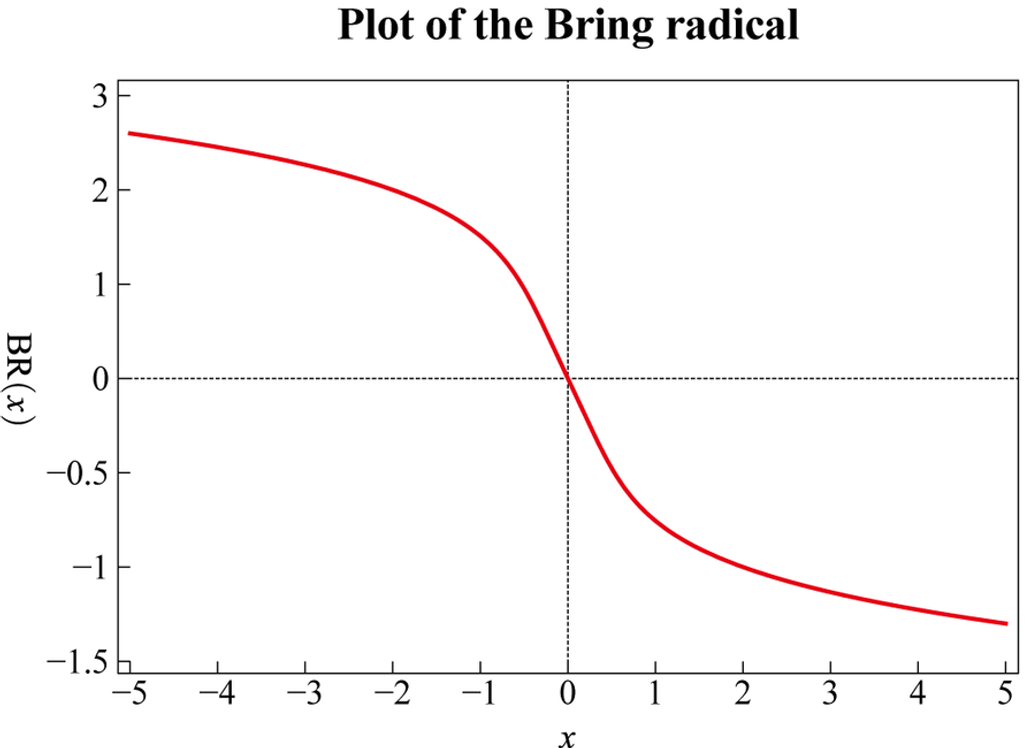
파일:브링근호_그래프_NeW.png

테일러 급수로 전개하면 다음과 같다.

[math(\displaystyle \mathrm{BR}(-x) = \sum_{k=0}^{\infty} \dbinom{5k}{k}\frac{(-1)^{k} x^{4k+1}}{4x+1})]

여기서 [math( \binom{5k}{k})]는 조합이다.

원점 대칭인 홀함수[2]로, 다음이 성립한다.

[math(\mathrm{BR}(x) = -\mathrm{BR}(-x))]
[2] 일반적인 홀함수와는 달리 [math(x > 0)]인 경우 [math(\mathrm{BR}(x) < 0)], [math(x < 0)]인 경우 [math(\mathrm{BR}(x) > 0)]이다.

주 활용처는 5차 이상의 고차방정식의 풀이로, 닐스 헨리크 아벨이 5차 방정식의 일반해를 구할 수 없다고 증명한 이래 뭇 수학자들이 여러 연구를 통해 찾아낸 것이다. 수학자 브링(Bring)은 모든 5차방정식이 [math(x^5+x+a=0)] 형태로 변환될 수 있다는 것을 보여주었다.

울프럼알파에서는 [math(\mathrm{BR})] 대신 5를 변형한 듯한 모양의 근호를 독자적으로 만들어 쓰는 듯하다.

도함수는 역함수의 미분법 또는 음함수의 미분법을 이용하여 다음과 같이 표현할 수 있다.

[math(\dfrac{\rm d}{{\rm d}x}\mathrm{BR}(x) =- \dfrac{1}{5[ \mathrm{BR}(x) ]^4+1})]

[증명]
---
해당 함수의 정의에 따라 [math(y^5 + y + x=0)]이다. 음함수의 미분법을 써 양변을 미분하면

[math(\begin{aligned} 5y^4 \dfrac{{\rm d}y}{{\rm d}x} + \dfrac{{\rm d}y}{{\rm d}x} + 1&=0 \\ (5y^4+1)\dfrac{{\rm d}y}{{\rm d}x}&=-1 \end{aligned})]

따라서

[math(\begin{aligned} \dfrac{\mathrm d}{\mathrm {d} x}\mathrm{BR}(x)&=-\dfrac{1}{5y^4 +1}\\&=-\dfrac{1}{5[\mathrm{BR}(x) ]^4+1} \end{aligned})]


역도함수는 역함수의 적분법을 이용한다.

[math(\displaystyle \int \operatorname{BR}(x)\,{\rm d}x = - \frac{[ \operatorname{BR}(x) ]^6 + 3 [ \operatorname{BR}(x) ]^2}{6} + x \operatorname{BR}(x) + x + {\sf const.})]

[math(\sf const.)]는 적분상수이다.


파일:크리에이티브 커먼즈 라이선스__CC.png 이 문서의 내용 중 전체 또는 일부는 2023-12-01 12:25:01에 나무위키 브링 근호 문서에서 가져왔습니다.

관련 문서